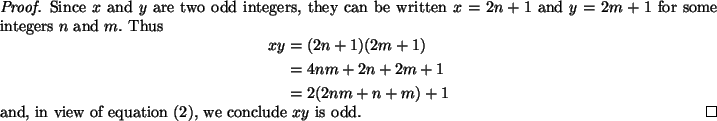Next: Prime Numbers
Up: What is a Number?
Previous: The Natural Numbers
The Integers
Every integer can be expressed as the difference between two natural numbers. In fact we introduce
the integers
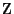 as the set of equivalence classes under the following
equivalence relation on
as the set of equivalence classes under the following
equivalence relation on
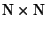 :
:
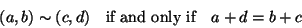 |
(1) |
Remark 2.1
Every integer
x can be expressed in the form
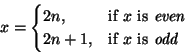 |
(2) |
for some integer
n.
Theorem 2.2
The product of two odd integers is an odd integer.
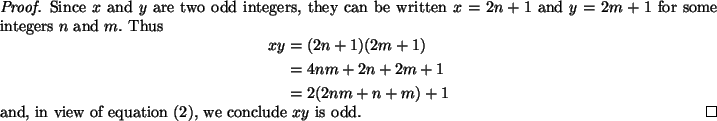
Table 1:
Products of Integers
| product |
even |
odd |
|---|
| even |
even |
even |
|---|
| odd |
even |
odd |
|---|
|
We leave it as an exercise for reader to prove that the product of an even
integer with any integer is even and we summarize this in a
Table 1.





Next: Prime Numbers
Up: What is a Number?
Previous: The Natural Numbers
Marc Fabbri
1999-10-25
![]() as the set of equivalence classes under the following
equivalence relation on
as the set of equivalence classes under the following
equivalence relation on
![]() :
: