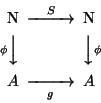
- 1.
- S is injective
- 2.
-
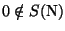
- 3.
- If a subset
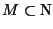 contains 0 and is mapped into itself by S then
contains 0 and is mapped into itself by S then
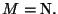
Die ganzen hat der liebe Gott gemacht, alles andere ist Menschenwerk. [God made the whole numbers, all the rest is the work of Man.] (KRONECKER, Jahresber. DMV 2, S. 19)
The existence of the natural numbers depends on the axiom of infinity, [E+91], and the uniqueness is gauranteed by the following result [Ded88].