S. Antontsev
Universidad da Beira Interior,
Covilh $\widetilde{a}$ , Portugal

and

S. Shmarev
Universidad de Oviedo, Spain

Parabolic equations with anisotropic non-uniform degeneracy

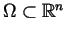Let $\Omega\subset \mathbb{R}^n$ be a bounded domain with Lipschitz-continuous boundary $\Gamma$ and $Q=\Omega\times (0,T]$ . We study the parabolic equations with anisotropic non-uniform degeneracy

$\begin{displaymath} u_t-\sum\limits_{i=1}^nD_{i}\left(a_i(x,t,u)\vert D_{i}u\ver... ...(x,t,u)\vert u\vert^{\sigma(x,t)-2}u=f(x,t)\quad\ {\rm in}\ Q, \end{displaymath}$

(1)

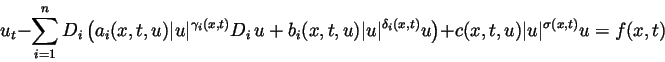$\begin{displaymath} u_{t}-\sum\limits_{i=1}^{n}D_{i}\left(a_{i}(x,t,u) \vert u\v... ...ta_i(x,t)}u\right) +c(x,t,u)\vert u\vert^{\sigma(x,t)}u=f(x,t) \end{displaymath}$

(2)

under the boundary and initial conditions

$\begin{displaymath} {u=0\ {\rm on}\ \Gamma}, \qquad {u(x,0)=u_{0}(x)\ {\rm in}\ \Omega}. \end{displaymath}$

(3)

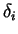The coefficients $\gamma_i$ , $\delta_i$ ,

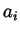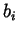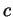and $\sigma$ are given functions of their arguments. Such equations emerge from the mathematical modelling of electro-rheological fluids, fluids with temperature-dependent viscosity, the processes of filtration in inhomogenenous anisotropic media. It is assumed that the coefficients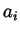

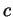are bounded,

, $c\geq 0$ , and the exponents

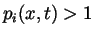, $\sigma(x,t)>1$ are continuous in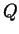

with a logarithmic module of continuity.

We prove the existence and uniqueness of weak solutions of problems (1), (3) and (2), (3) and study the localization (vanishing) properties of weak solutions and the effect of finite time stabilization of solutions to a stationary profile. The study of the localization properties is performed with the method of local energy estimates [2]. The detailed proofs can be found in [1,3,4,5]

Next: Bibliography