Let 
be the operator
Then the adjoint of with respect to the standard inner products
in 
and 
is the operator
Our homogeneous and self-dual linear feasibility model for SDP is based on those appearing in [11] for linear programming (LP). It has the following form:
where 
are positive semidefinite. A solution to this system
with 
positive either gives optimal solutions to the SDP and
its dual or gives a certificate of primal or dual infeasibility.
At each iteration of our algorithms, we apply Newton's method to a perturbation of equation (22), namely,
where the right-hand side quantities are considered as fixed.
Here 
and 
are parameters, and 
and 
are
defined in (26) and (25) below, respectively.
Just as in the case of infeasible path-following methods,
the search direction
at each iteration of our homogeneous algorithms
is computed from a symmetrized Newton equation
derived from the perturbed equation (23):
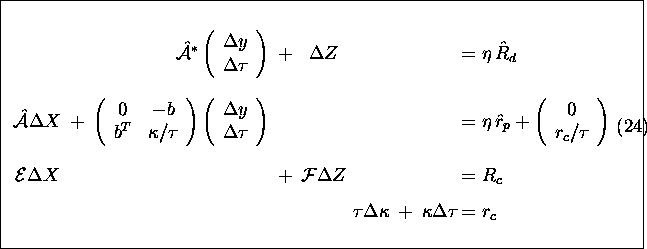where 
and 
, 
are defined as in (6)
and (7), respectively, and
We compute the search direction via a Schur complement
equation as follows. First compute 
from the
equation
where
Then compute 
, 
, and 
from the equations
