Part 4

1. Find the interval of convergence (you must test endpoints, if applicable) of the following series.
   
   $$\sum_{n=0}^{\infty } 2^{-n} \left( 2x-1 \right )^n$$
   
   

   Solution: $-1/2 < x < 3/2$

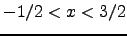
2. Find a power series representation, and the interval on which it represents the function, for
   
   $$f(x)= \frac{x^2}{4-x^2}$$
   
   

   Solution: $\sum_{n=0}^{\infty} \frac{x^{2n+2}}{4^{n+1} }$, $-2<x<2$

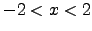
3. Find the Taylor series centered at 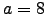$a=8$ for
   
   $$f(x)=\sqrt[3]{x}$$
   
   

   Solution:
   

   $$2 +\frac{1}{12} (x-8) +\sum_{n=2}^{\infty} \frac{(-1)^{n-1}2\cdot 5 \cdots (3n-4)}{3^n 2^{3n-1} n! } (x-8)^n$$
   
   

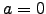4. Using Taylor's Inequality, determine an upper bound for the error in approximating $f(x)=e^{-2x}$ by its Taylor polynomial $T_2(x)$, centered at $a=0$, on the interval $[-1/4,1/4]$.

   Solution: $\frac{\sqrt e}{48}$