Practice Exam 1

1. Determine if the following sequence converges or diverges. If it converges find the limit.
   
   $$a_n=\sqrt{n+2}-\sqrt{n}$$
   
   

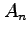2. Approximate the sum of the following series to within $0.02$ using $A_n$ for the approximation via the integral test.
   
   $$\sum_{n=1}^{\infty} \frac{1}{n^3}$$
   
   

3. Let $a_1=1, a_{n+1}=\frac{1}{3}(a_n+4)$
   1. Assuming that the sequence converges, find the limit.
   2. Prove, using mathematical induction, that the sequence is bounded.
   3. Prove, using mathematical induction, that the sequence is monotonic.
   4. Determine whether the sequence converges or diverges.

4. Determine if the following series converges or diverges. If it converges find the sum.
   
   $$\sum_{n=1}^{\infty} (-5)^{1-n} (\pi)^{n}$$
   
   

5. Determine if the following series converges conditionally, converges absolutely, or diverges.
   
   $$\sum_{n=1}^{\infty} \frac{\sin^n n}{n^n}$$
   
   

6. Determine if the following series converges or diverges.
   
   $$\sum_{n=1}^{\infty} n e^{-n^2}$$
   
   

7. Determine if the following series converges conditionally, converges absolutely, or diverges.
   
   $$\sum_{n=1}^{\infty} \frac{\cos(\pi n)}{n}$$
   
   

8. Determine if the following series converges or diverges.
   
   $$\sum_{n=1}^{\infty} \sin ^2 n \ e^{-n}$$