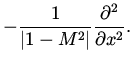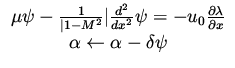Next: Three Dimensional Case
Up: Small Disturbance Potential Equation
Previous: Small Disturbance Potential Equation
In this case  does not exists and we
have a symbol
does not exists and we
have a symbol
 |
|
|
(51) |
This is the symbol of the differential operator
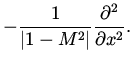 |
|
|
(52) |
A preconditioned gradient descent method have the form
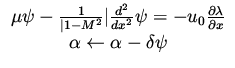 |
|
|
(53) |
That is, we have to solve an ODE on the boundary with the gradient as a source
term, before using it as a direction of change for the design variable.
According to our analysis the new method converges at a rate with
is independent of the number of design variables, since the symbol for
the modified iteration does not depend on  .
Note that the construction of the preconditioner was done on the differential
level but the numerical implementation is using some approximation of it, e.g.,
finite difference approximation.
.
Note that the construction of the preconditioner was done on the differential
level but the numerical implementation is using some approximation of it, e.g.,
finite difference approximation.



Next: Three Dimensional Case
Up: Small Disturbance Potential Equation
Previous: Small Disturbance Potential Equation
Shlomo Ta'asan
2001-08-22