---

11.2.14
I will write rn for the square root of n. Q(r2,r3,r5)
Gal_Q(Q(r2,r3,r5)) is isomorphic to Z2xZ2xZ2 via the isomorphism f(t)=(a,b,c) where a=0 if t(r2)=r2, a=1, if t(r2)=-r2,
b=0 if t(r3)=r3, b=1, if t(r3)=-r3, c=0 if t(r5)=r5, c=1, if t(r5)=-r5.

---

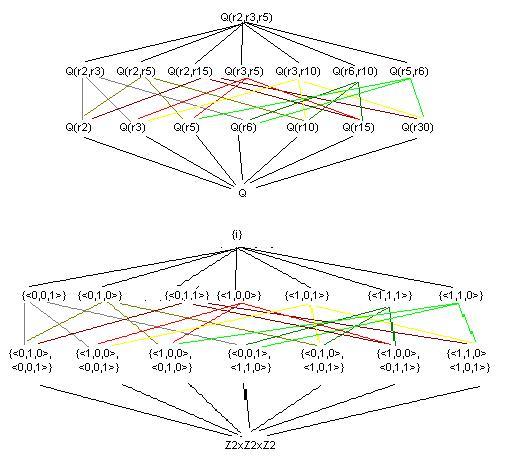
11.3.1a
The sequence Q, Q(r7), Q(r7,r5), Q(r7,r5,rr(1+r7)), Q(r7,r5,rr(1+r7)),rr(2+r5)) shows that Q(r7,r5,rr(1+r7)),rr(2+r5)) is a radical extension of Q. Clearly rr(1+r7))-rr(2+r5) is in Q(r7,r5,rr(1+r7)),rr(2+r5)).

---

11.3.3
Suppose K is a radical extension of F. Then there are sequences F=F₀,F₁,...,F_n=K and u₁,...,u_n-1 s.t. F_i(u_i)=F_i+1. And for some power n_i-1 of u_i-1 is in F_i-1. This means that u_i is a root of a polinomial of the form x^(n_i)-a where a is in F_i. This means [F_i:F_i-1] is at most n_i-1. [K:F]=[F_n:F_n-1]...[F₁:F] is less than n₀n₁...n_n-1 so [K:F] is finite.

---

11.3.5a
Easy to check that H is normal in A₄. We know A₄ is normal in S₄ and |S₄/A₄|=2, therefore S₄/A₄=Z2 so is abelian. |A₄/H|=[A₄:H]=3, so A₄/H=Z3. Obviously {e} is normal in H and H is of order 4 so it must be Z4 or Z2xZ2. Both are abelian. So the sequence S₄,A₄,H,{e} shows that S₄ is solvable.

---

11.3.7e
6'th roots of unity are cos(2tPi/6)+ isin(2tPi/6), where t is in {0,1,2,3,4,5}. By substituting t will get the 6'th roots of unity are: +/- 1 , (+/- 1 +/- i sqrt(3))/2