Introduction to Numerical Python

What is “Numerical Python”?

  • A collection of many libraries to make numerical computation easier.

    • NumPy: $N$-dimensional arrays, fast linear algebra

    • SciPy: Optimization, interpolation, statistics, special functions, …

    • SymPy: Symbolic computation

    • MatPlotLib: Data visualization, plotting

    • Pandas: Data analysis

  • Various others: TensorFlow, PyTorch for Machine Learning, …

Why NumPy?

  • Python Sucks

    • Python is slow (interpreted, dynamically typed).

    • Parallelization limited by the Global Interpreter Lock

  • Long live Python

    • Use multiprocessing / memhive to sidestep the Global Interpreter Lock

    • Use fast optimized libraries to do the bulk of the work. (NumPy, etc)

    • Python provides an easy to learn/use interface.

Numpy Fundamentals

  • Python list: One dimensional, can expand / grow.

  • NumPy array (aka ndarray): Fixed size; multiple dimensions.

    >>> a = np.array( [ [1,2,3], [4,5,6] ] )
>>> a
array([[1, 2, 3],
       [4, 5, 6]])
>>> a.shape
(2, 3)
>>> a[1,2]
np.int64(6)

  • Array operations: Operators act on arrays element-wise:

    >>> a ** 2
array([[ 1,  4,  9],
       [16, 25, 36]])
>>> a + 1
array([[2, 3, 4],
       [5, 6, 7]])

Slicing / iterating

  • Slicing works as expected

    a[1, :] # [4, 5, 6] (second row)
a[:, 0] # [1, 4] (first column)
a[1]    # Equivalent to a[1, :]

  • Use a[..., m:n:s, ...] in any position

    • Extracts every $s^\text{th}$ element from m (inclusive) to n (exclusive).

  • Iterating is done over the first axis:

    for r in a: # iterates over rows a[0], a[1], ...
for x in a[1]: # interates over column a[1, 0], a[1, 1], ...

Universal functions

  • math functions don’t act on arrays:

    math.sin(a) # Error

  • NumPy functions act on arrays element wise:

    np.sin(a)   # gives [ sin(a[0]), sin(a[1]), ... ]

  • NumPy functions also act on scalars

    np.sin(0)   # works
math.sin(0) # works

  • See NumPy documentation on universal functions

Extremely convenient for numerical work

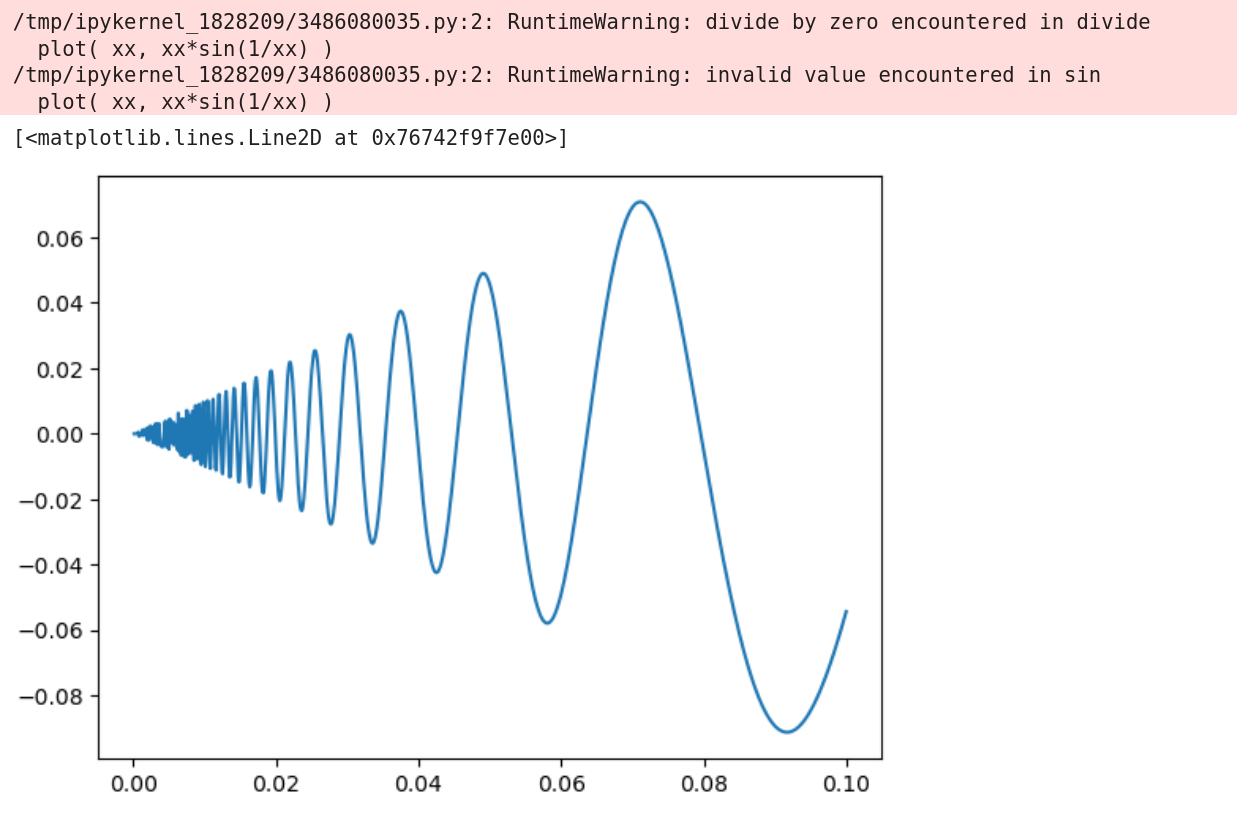
  • Regular python

    for i in range( N ):
    x = 0.1*i/N
    plot( x, x*math.sin(1/x) )
# Division by 0 exception

  • NumPy:

    xx = np.linspace( 0, 2*pi, N )
plot( xx, xx*np.sin(1/xx) )
# Runtime warning, but works
Numpy Output

Using NumPy

  • Option 1: %pylab inline (Quick and dirty MatLab type environment)

    • Imports all functions from matplotlib.pylab and numpy
    • Replaces Python sum with numpy.sum
    • Depreciated; but very useful if you just want a quick plot / scratch.

  • Option 2: Import the functions you want.

    %matplotlib inline
# Another option is `%matplotlib widget`
import numpy as np, matplotlib as mpl, scipy as sp
from matplotlib import pylab, mlab, pyplot as plt
from matplotlib.pylab import plot, scatter, contour
from tqdm.notebook import tqdm, trange

from numpy import sqrt, pi, exp, log, floor, ceil, sin, cos
from numpy.linalg import norm

rng = np.random.default_rng()

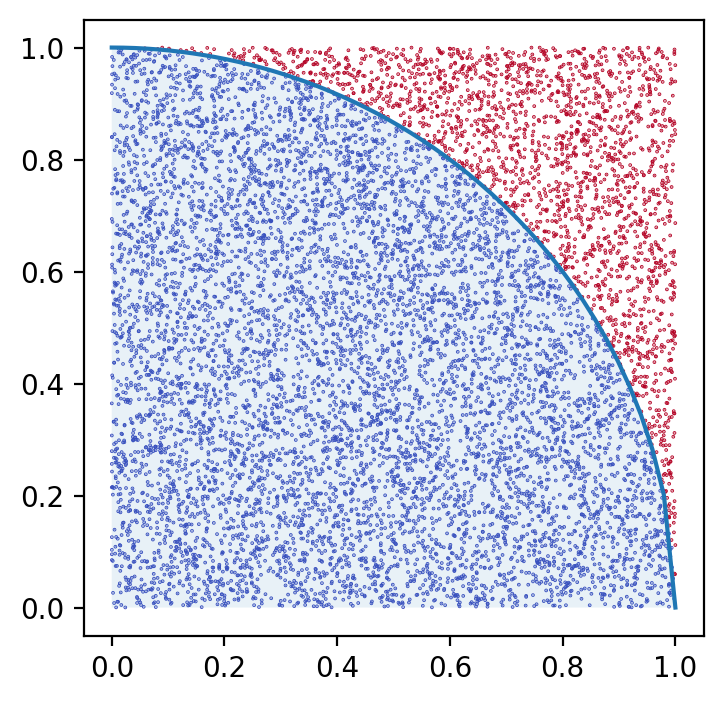
Monte Carlo compute $\pi$

  • $U \sim \Unif([0,1]^2)$

  • $\P( \abs{U} < 1 ) = \frac{\pi}{4}$

  • Compute $\displaystyle \frac{1}{N} \sum_1^N \one_{\set{\abs{U_i} < 1}}$.

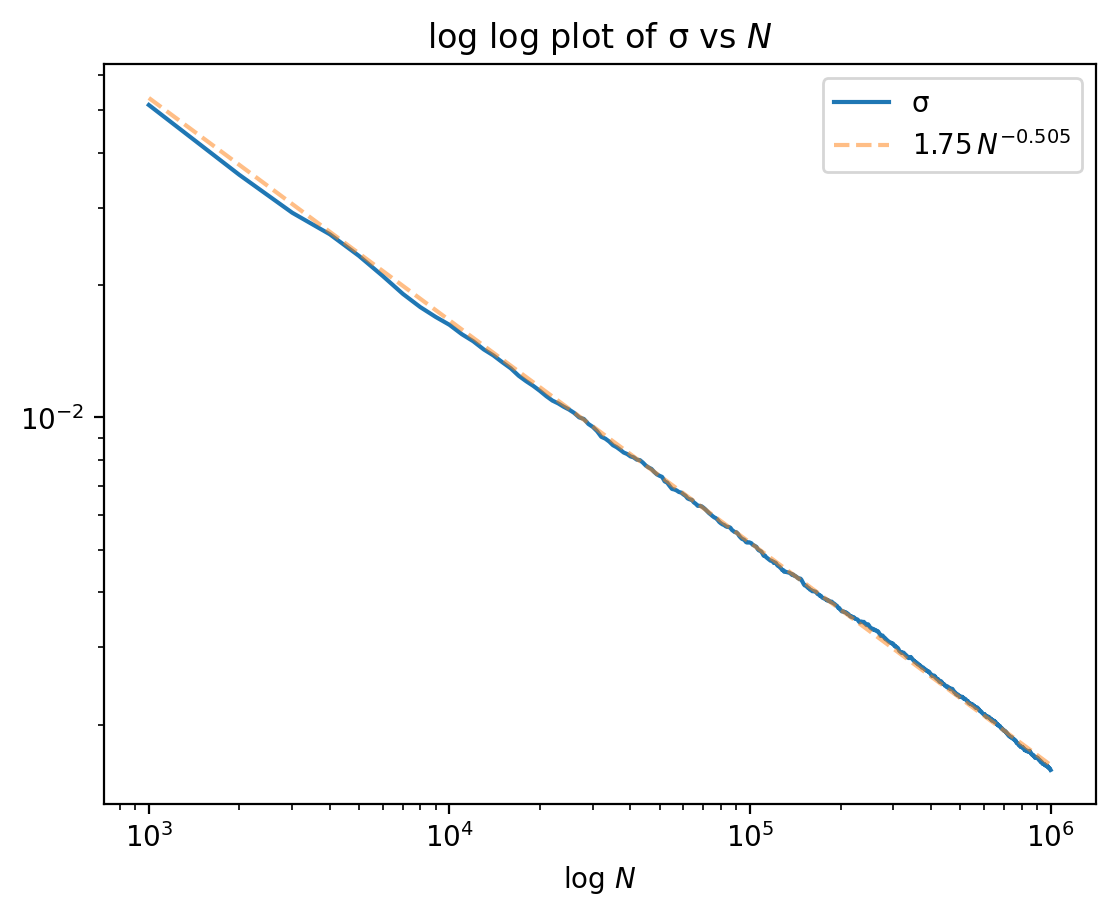
    • Approximates $\pi$ with an $O(1/\sqrt{N})$ error

Checking performance

  • Set N = 10**7

  • “First” implementation: (took 33.31s) 

    n_inside = 0
for i in trange(N):
    (U1, U2) = (rng.uniform(), rng.uniform())
    if sqrt(U1**2 + U2**2) < 1:
        n_inside += 1

  • Implementation with NumPy functions: (took 0.195s) 

    U = rng.uniform( size=(2, N) )
n_inside = np.sum( norm( U, axis=0 ) < 1 )

  • Use library functions as much as you can.

  • Avoid Python loops as much as possible.

Don’t run out of memory

  • Easy to set $N = 10^9$, and run U = rng.uniform( size=(2, N) )

  • Takes 15Gb memory to store. May crash your computer

  • Run code in chunks:

    N = 10**9
M = 1000
n_inside = 0
for i in trange(M):
    U = rng.uniform( size=(2, N//M) )
    n_inside += np.sum( norm( U, axis=0 ) < 1 )

  • Can trivially parallelize chunks.

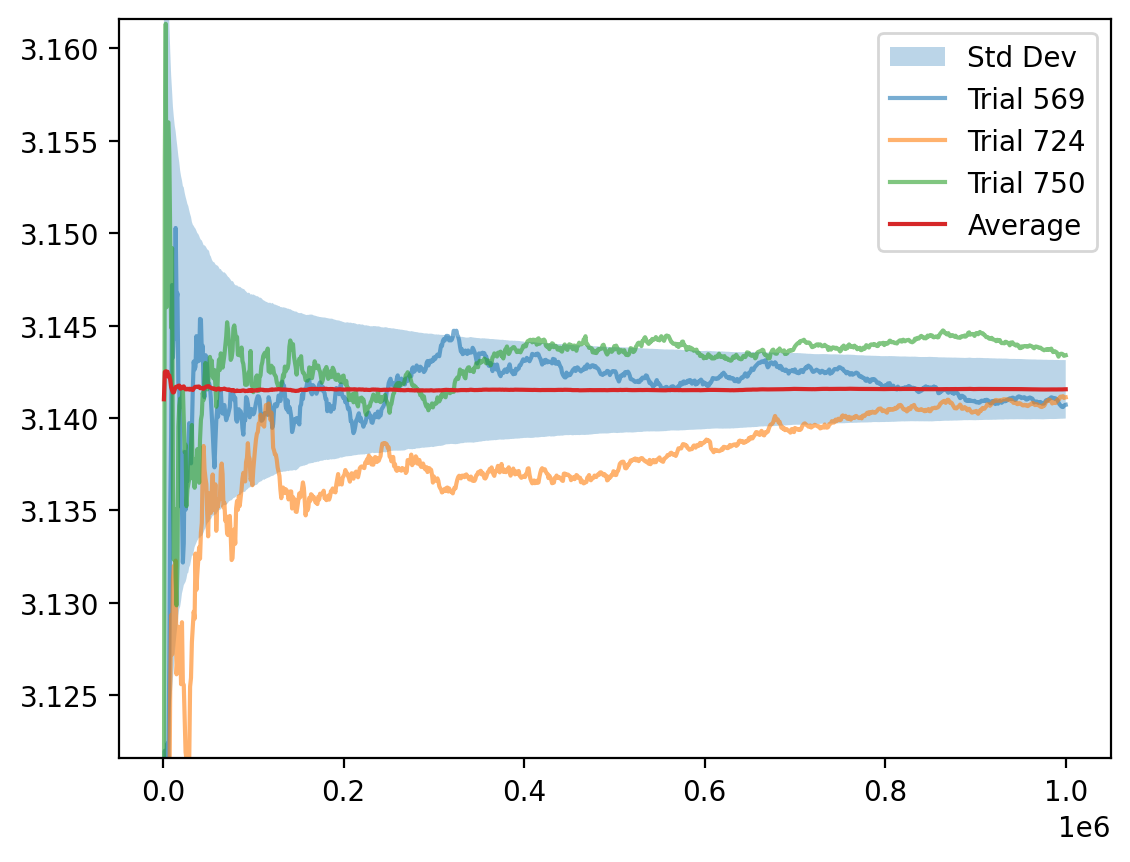
Estimate of $\pi$ as $N \to \infty$.

for n in trange( n_iters ):
    U = rng.uniform( size=(2, M, n_trials) )
    n_inside = np.sum( norm( U, axis=0 ) < 1, axis=0 )
    hat_π[n] = 4*n_inside
hat_π = (np.cumsum( hat_π, axis=0 ).T / NN).T

Checking error scales like $O(1/\sqrt{N})$

# Use `polyfit` to fit $\log(σ)$ to $a + b N$.
plt.loglog( NN, σ, label='σ' )

a = np.polyfit( log(NN), log(σ), 1 )
plt.loglog( NN, exp( a[0]*log(NN) + a[1] ), '--',
    alpha=.5, label=f'${exp(a[1]):.2f}\\, N^{{{a[0]:.3f}}}$' )

Volume of a $d$-dimensional ball

  • Suppose $U \sim \Unif( [0, 1]^d )$. Then $\displaystyle \P( \abs{U} < 1 ) = \frac{\vol( B(0, 1) )}{2^d}$

  • Exact formula: $\displaystyle \vol(B(0, 1)) = \frac{\pi^{d/2}}{\Gamma(\frac{d}{2}+1)}$

  • Easy to implement:

    for d in trange( 1, D ):
    vol[d] = pi**(d/2) / sp.special.gamma( d/2 + 1 )

    U = rng.uniform( size=(d, N) )
    n_inside = np.sum( norm(U, axis=0) < 1 )
    hat_vol[d] = 2**d * n_inside/N

Curse of dimensionality

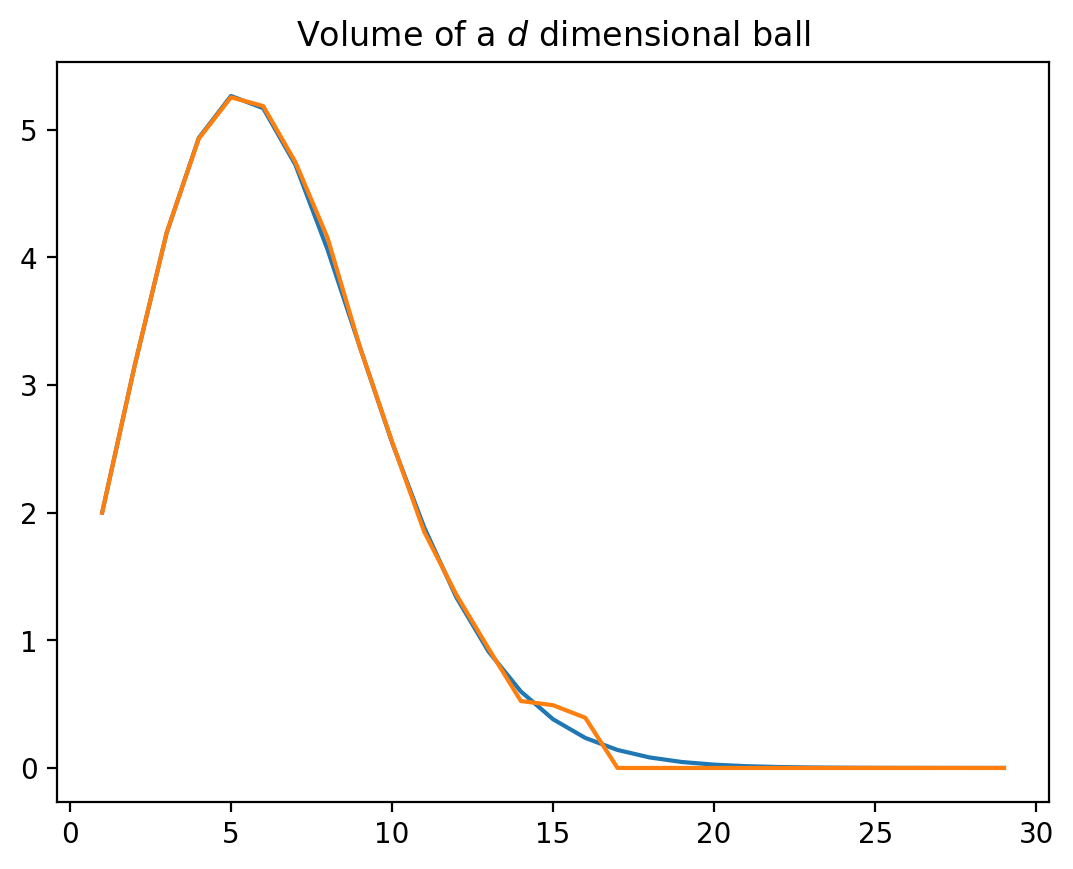
Simulations don’t find even one point inside $B(0,1)$ in high dimensions.

Problem: Generate a Rejection Sample plot

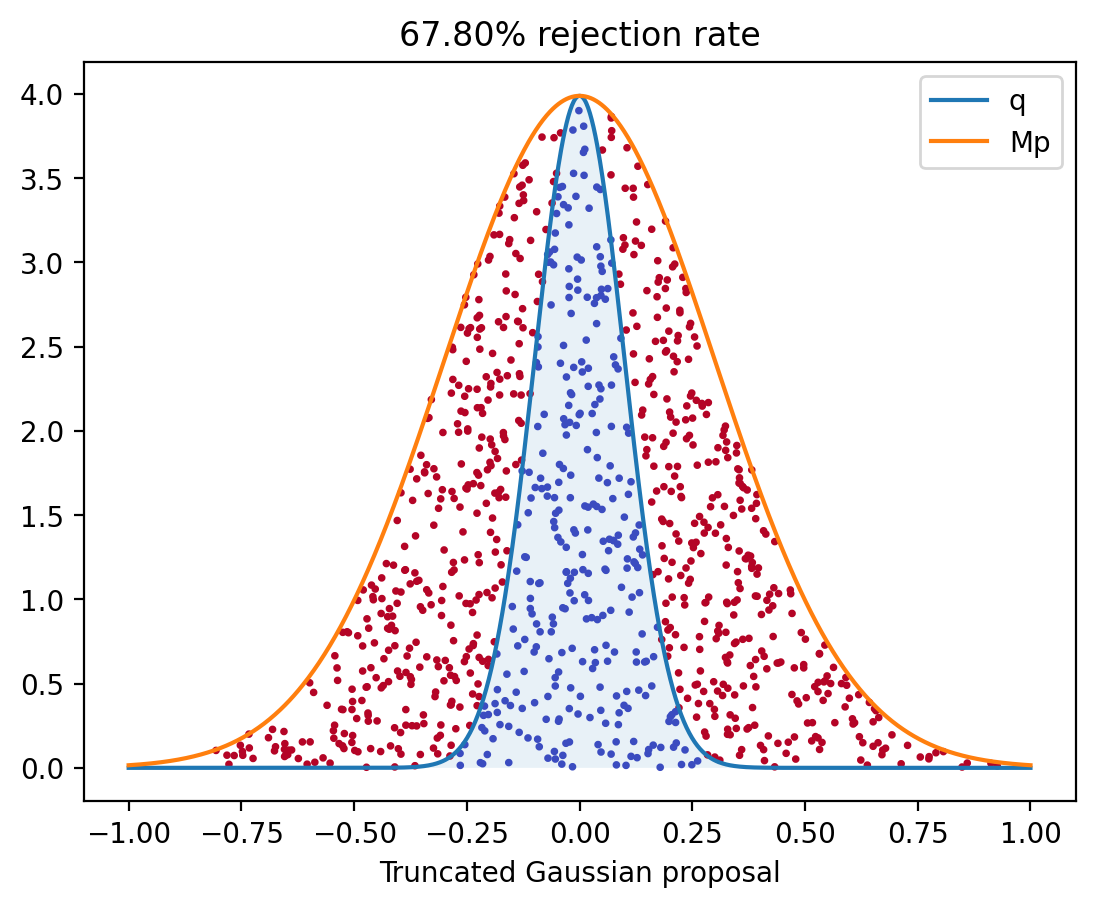
  • Points above the graph of $q$ (in red) are rejected
    A bad implementation is to:

    1. Sample one $X \sim p$, one $U \sim \Unif([0, 1])$.

    2. Set color=red if $Mp(X) > q(X)$.

    3. Set color=blue otherwise.

    4. plot( X, M p(X), color )

    5. Repeat 1,000 times.

  • Try to vectorize this and plot without looping.

Problem: Numerically finding the PDF/CDF

  • Say X has N samples from some distribution.

  • Problem: Numerically approximate the CDF and PDF.

  • Algorithm for computing the CDF:

    • Say the points are $x_1, \dots, x_N$ with $x_1 < x_2 \cdots < x_N$.

    • Know $F(x_k) = k/N$. Find $F$ at other points by interpolating.

  • Implement this so you get acquainted with NumPy/SciPy:

Numerical approximation of the CDF

CDF

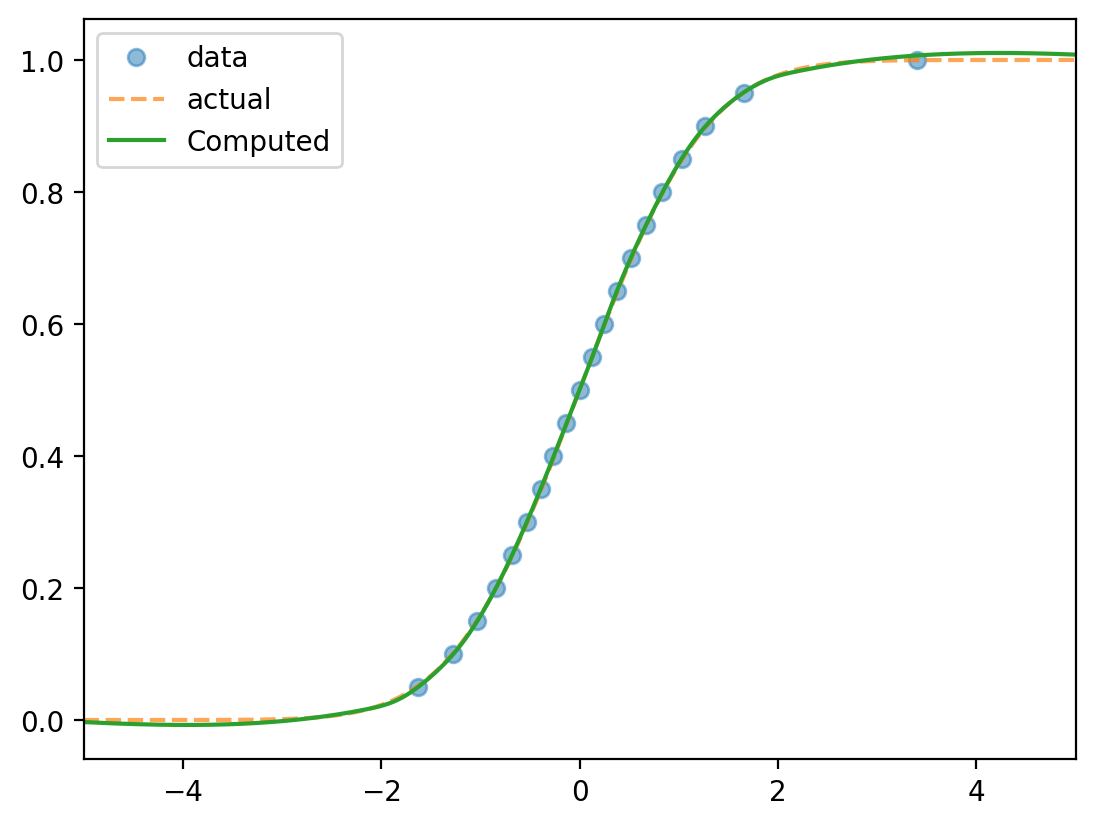
Data: 10,000 samples from $N(0, 1)$

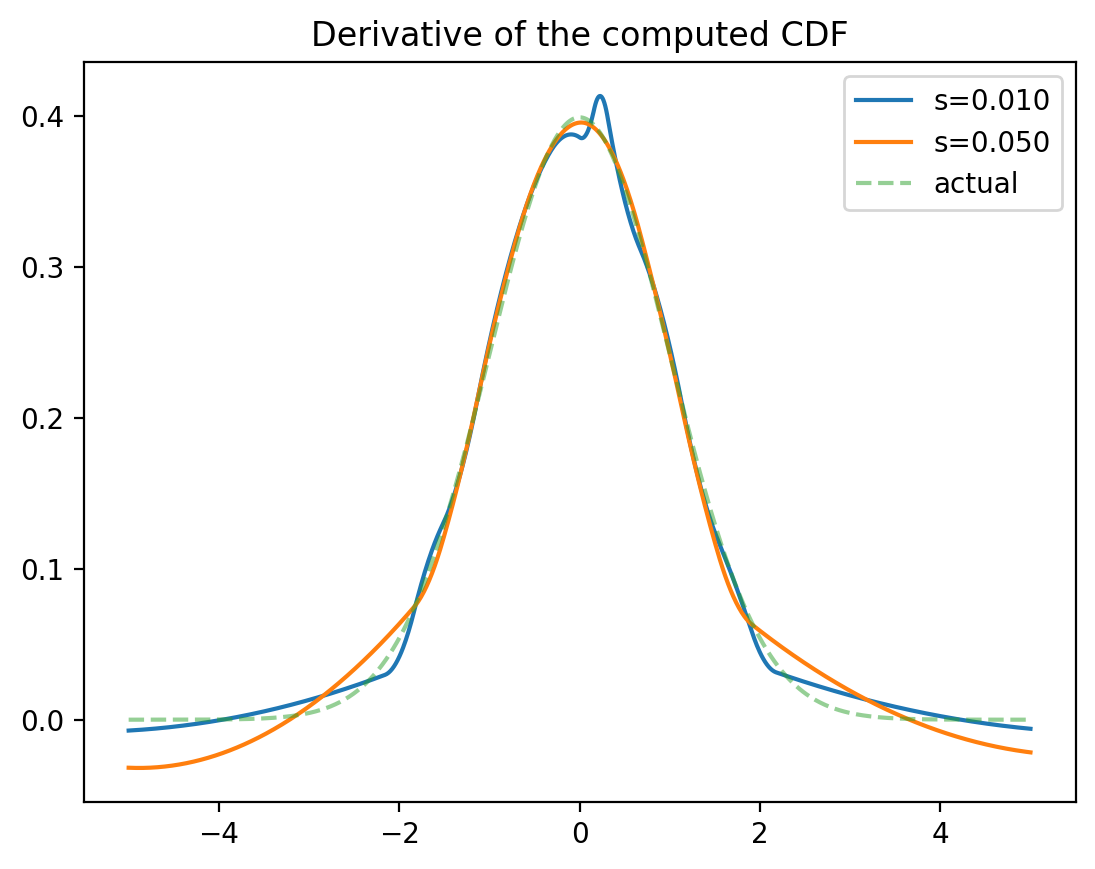
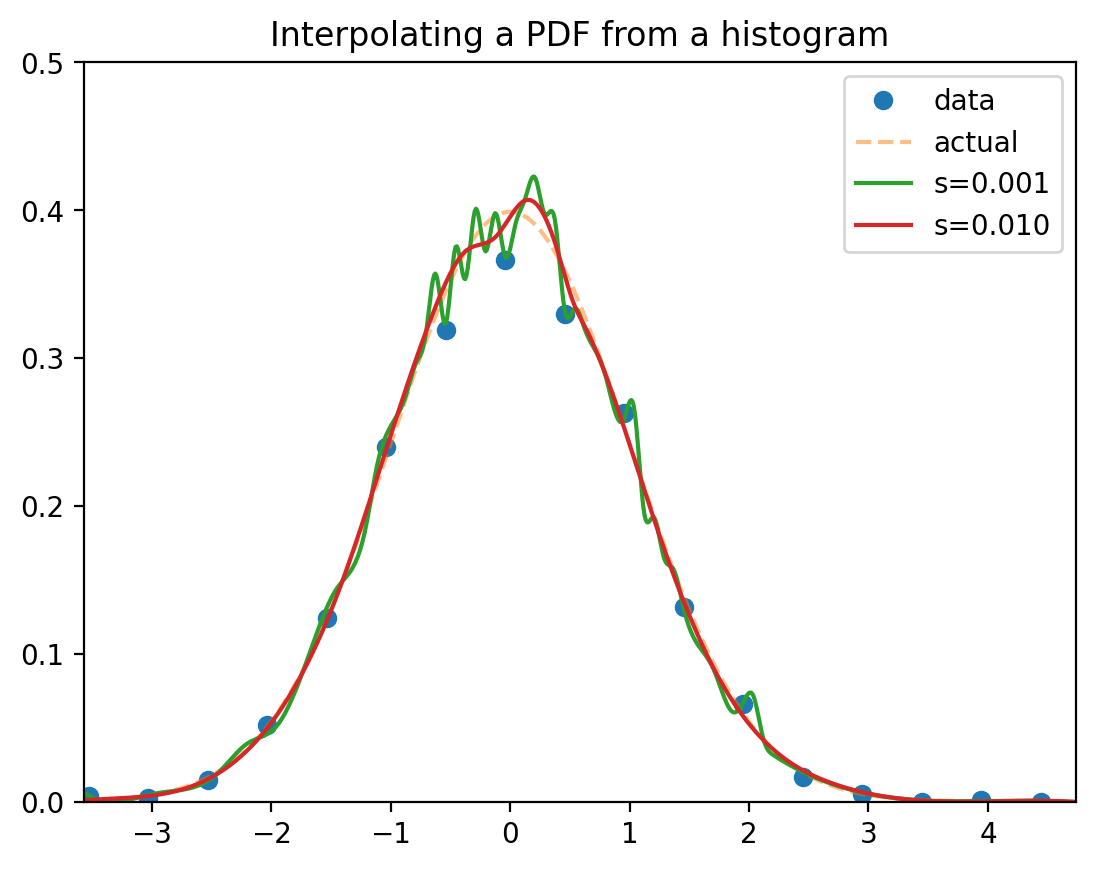
Numerically finding the PDF

  • Option 1: Differentiate the CDF (use UnivariateSpline.derivate)

  • Option 2: Create a histogram.

    • numpy.histogram divides the data into bins

    • Assume the PDF at bin midpoints is proportional to the counts

    • Interpolate and smooth.

Numerical approximation of the PDF

PDF, by differentiating the CDF PDF, from a histogram

Few concluding tips

  • Jupyter Notebooks make it easy to run simulations interactively.

  • Online documentation is excellent.

  • Shift+Tab / Ctrl+I / right click for contextual help

  • Use library functions. Don’t reinvent the wheel.

    • scipy.random samples from most common distributions
    • scipy.interpolate has curve fitting / interpolation functions
    • scipy.linalg, numpy.linalg various linear algebra functions

  • Use vectorized functions; avoid loops as much as possible.

  • Notebook with code from these slides is here.