


Next: About this document ...
documentclass[10pt,twoside]article
usepackageamsfonts,amsfonts,amsthm,amssymb,amsmath
numberwithinequationsection
setlengthtextwidth6.5in
setlengthtextheight9in
setlengthoddsidemargin0in
setlengthevensidemargin0in
setlengthtopmargin-0.5in
par
newedtheoremtheoremTheorem[section]newedtheoremlemma[theorem]Lemmanewedtheoremproposition[theorem]Propositionnewedtheoremcorollary[theorem]Corollarynewedtheoremremarks[theorem]Remarksnewedtheoremremark[theorem]Remarknewedtheoremdefinition[theorem]Definitionnewedcommandrrmathbb R
newedcommandAImathbb A
newedcommandNmathbb N
newedenvironment@abssec[1]par
if@twocolumn
par
csname section*endcsname#1par
else
par
vspace.05infootnotesize
par
parindent .2in
par
upshapebfseries #1. ignorespaces
par
fi
par
if@twocolumnelsepar
vspace.1infi
par
newedcommandkeywordsnameKey words:
par
newedcommandAMSnameAMS subject classification
par
newedenvironmentkeywordspar
if@twocolumn
par
section*keywordsnamepar
else
par
vspace.05infootnotesize
par
parindent .2in
par
upshapebfseries keywordsname. ignorespaces
par
fi end@abssec
par
newedenvironmentAMSpar
if@twocolumn
par
section*AMSnamepar
else
par
vspace.05infootnotesize
par
parindent .2in
par
upshapebfseries AMSname. ignorespaces
par
fi end@abssec
par
begindocument
par
beginabstract
In part I, it is shown that for integrals of the type
beginequation*
I(u,v):=int_Omega f(x,u(x),v(x))dx,
endequation*
with
open, bounded, and
 Carathéodory satisfying a growth
condition
Carathéodory satisfying a growth
condition
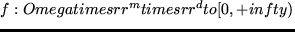 , for some
, for some
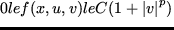 , a sufficient condition for lower semicontinuity along
sequences
, a sufficient condition for lower semicontinuity along
sequences 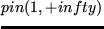 in measure,
in measure,
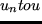 in
in 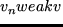 ,
,
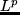 in
in 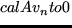 is the
is the 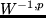 -quasiconvexity of
-quasiconvexity of
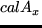 . Here
. Here 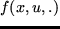 is a variable coefficients operator of the
form
beginequation*
cal A:= sum_i=1^N A^(i)(x)frac partial partial x_i,
endequation*
with
is a variable coefficients operator of the
form
beginequation*
cal A:= sum_i=1^N A^(i)(x)frac partial partial x_i,
endequation*
with
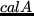 ,
, 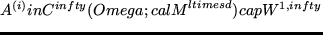 , satisfying the condition
beginequation*
rm rankleft( sum_i=1^N A^(i)(x)omega_i right)=rm constquad textfor
, satisfying the condition
beginequation*
rm rankleft( sum_i=1^N A^(i)(x)omega_i right)=rm constquad textfor
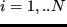 and
and
 ,
endequation*
and
,
endequation*
and 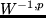 denotes the constant coefficients operator one obtains by freezing
denotes the constant coefficients operator one obtains by freezing 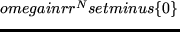 . Under additional regularity conditions on
. Under additional regularity conditions on 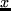 it is proved that the condition above is also necessary.
A characterization of the Young measures generated by bounded sequences
it is proved that the condition above is also necessary.
A characterization of the Young measures generated by bounded sequences 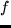 in
in 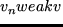 satisfying the condition
satisfying the condition
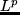 in
in 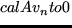 is obtained.
par
In part II, an integral representation for the functional
beginequation*
aligned
cal F(m,M):= rm inf left{ liminf_k to +infty int_Omega f(x,m_k(x),nabla m_k(x))dx + int_Omegacap S(m_k) |[m_k](x)|dcal H^N-1 :right.
is obtained.
par
In part II, an integral representation for the functional
beginequation*
aligned
cal F(m,M):= rm inf left{ liminf_k to +infty int_Omega f(x,m_k(x),nabla m_k(x))dx + int_Omegacap S(m_k) |[m_k](x)|dcal H^N-1 :right.
left.m_k in SBV(Omega;rr^N),quad |m_k(x)|=1quadtexta.e. in 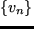 ,right.
,right.
left. m_k to mquad textinquad L^1(Omega;rr^N),quad
nabla m_k weak Mquad textinquad L^2(Omega; rr^N)right}
endaligned
endequation*
is obtained. This problem is motivated by equilibrium issues in micromagnetics.
par
In part III, the effective behavior of second order strain energy densities is
obtained using relaxation and 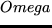 convergence techniques. The
Cosserat theory is recovered within a dimension reduction analysis
for
convergence techniques. The
Cosserat theory is recovered within a dimension reduction analysis
for 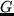 thin domains with varying profiles. Homogeneous and
inhomogeneous
thin domains with varying profiles. Homogeneous and
inhomogeneous 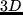 models with periodic profiles are treated.
par
endabstract
par
enddocument
models with periodic profiles are treated.
par
endabstract
par
enddocument



Next: About this document ...
Nancy J Watson
2003-07-07