We study the Dirichlet problem for the p(x)-Laplacian, in the case when the
variable exponent 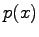 is infinite in a subdomain
is infinite in a subdomain 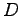 . The main issue is to
give a proper sense to what a solution is. To this end, we consider the limit
of the solutions
. The main issue is to
give a proper sense to what a solution is. To this end, we consider the limit
of the solutions 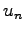 to the corresponding problem when
to the corresponding problem when
 , in particular, with
, in particular, with 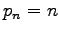 in
in 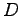 . Under suitable assumptions on
the data, we find that such a limit exists and that it can be characterized as
the unique solution of a variational minimization problem. Moreover, we
examine this limit in the viscosity sense and find an equation it satisfies.
. Under suitable assumptions on
the data, we find that such a limit exists and that it can be characterized as
the unique solution of a variational minimization problem. Moreover, we
examine this limit in the viscosity sense and find an equation it satisfies.