Michal Kowalczyk
University of Chile
Santiago, Chile
michal.kowalczyk@gmail.com
Nonlinear Schrödinger Equations:
Concentration on Weighted Geodesics in the Semi-Classical Limit
Abstract: We consider the problem
where 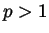 ,
,
 is a small parameter and
is a small parameter and 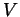 is a
uniformly positive, smooth potential. Let
is a
uniformly positive, smooth potential. Let  be a closed
curve, nondegenerate geodesic relative to the weighted arclength
be a closed
curve, nondegenerate geodesic relative to the weighted arclength
 , where
, where
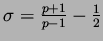 . We prove the existence of a
solution
. We prove the existence of a
solution
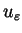 concentrating along
concentrating along  , and
exponentially small in
, and
exponentially small in
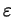 at any positive distance from
it, provided that
at any positive distance from
it, provided that
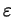 is small and away from certain
critical numbers. This proves a conjecture raised By Ambrosetti,
Malchiodi and Ni.
is small and away from certain
critical numbers. This proves a conjecture raised By Ambrosetti,
Malchiodi and Ni.