CARNEGIE MELLON UNIVERSITY
DEPARTMENT OF MATHEMATICAL SCIENCES
Integral Test Approximation
Dr. Timothy Flaherty
Let
 be a series which converges by the integral
test, with
be a series which converges by the integral
test, with  satisfying
satisfying  for all
for all  . We wish to estimate
the actual sum
. We wish to estimate
the actual sum  of the series. First approximate
of the series. First approximate  with a partial sum
with a partial sum
 ,
with error given by the remainder
,
with error given by the remainder
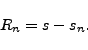 |
(1) |
As shown in the text,
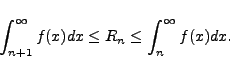 |
(2) |
Let
 , and
, and
 , so
, so
 . This estimate is sometimes not a very good
estimate, and may require many terms for a desired approximation. To improve
matters we define an approximation which involves both a partial sum and an
improper integral.
. This estimate is sometimes not a very good
estimate, and may require many terms for a desired approximation. To improve
matters we define an approximation which involves both a partial sum and an
improper integral.
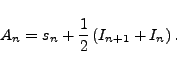 |
(3) |
The error in using  to approximate the actual sum
to approximate the actual sum  is given by
is given by
 . Now
. Now
We now simplify things by using the fact that  is decreasing, so
is decreasing, so
 on the interval
on the interval ![$[n,n+1]$](img18.png) . We obtain
. We obtain
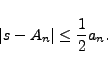 |
(4) |
This can be used to determine  so that
so that  is accurate to within the
desired amount
is accurate to within the
desired amount  . Perhaps a slightly smaller value could work -
but this is usually not so important. Try the following exercises where we apply
the above.
. Perhaps a slightly smaller value could work -
but this is usually not so important. Try the following exercises where we apply
the above.
- Approximate
 to within
to within
 using (4) to determine the value
using (4) to determine the value  to use in computing
to use in computing  in (3).
in (3).
- Use the fact that
 in the above to determine the
actual error,
in the above to determine the
actual error,  , for the approximation
, for the approximation  that you computed.
that you computed.
- Now determine the actual error when using
 , for your
value of
, for your
value of  .
.
- How many terms do you need to approximate
 to within
to within
 using only partial sums
using only partial sums  ?
?
Timothy J Flaherty
2006-04-03
![]() be a series which converges by the integral
test, with
be a series which converges by the integral
test, with ![]() satisfying
satisfying ![]() for all
for all ![]() . We wish to estimate
the actual sum
. We wish to estimate
the actual sum ![]() of the series. First approximate
of the series. First approximate ![]() with a partial sum
with a partial sum
![]() ,
with error given by the remainder
,
with error given by the remainder
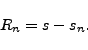
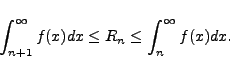

![]() is decreasing, so
is decreasing, so
![]() on the interval
on the interval ![]() . We obtain
. We obtain