The concept of a set is one of the most fundamental ideas in mathematics. Essentially, a set is simply a collection of objects. The field of mathematics that studies sets, called set theory, was founded by the German mathematician Georg Cantor in the latter half of the 19th century. Today the concept of sets permeates almost all of modern mathematics; almost every other mathematical concept (including the seemingly fundamental concept of numbers!) has been defined, directly or indirectly, in terms of sets.
A set is a collection of objects, considered as a mathematical object in its own right. (A helpful metaphor for a set is a cardboard box—the box can hold objects, and we can choose to think about the objects in the box individually, or to think about the box and its contents collectively as a single object.) The objects in a set are called the elements (or members) of the set; the elements are said to belong to the set (or to be in the set), and the set is said to contain the elements. Usually the elements of a set are other mathematical objects, such as numbers, variables, or geometric points.
A set is often written by listing its elements between curly braces { }. For example, a set containing the numbers 1, 2, and 3 would be written as {1, 2, 3}.
When the elements of a set follow an obvious pattern but there are too many of them to list explicitly, it is common to list the first few elements (to establish the pattern) and the last element (to specify where the pattern stops), with an ellipsis (…) in between to indicate that the elements in the middle were omitted. For instance, to write the set of positive integers from 1 to 100, we can write {1, 2, 3, …, 100}. If no element is written after the ellipsis, the pattern is assumed to continue forever; so the set written {1, 2, 3, …} contains all of the positive integers. Sometimes the elements of a set go on forever in both “directions”—for instance, the set of all integers (both positive and negative) can be written as {…, −3, −2, −1, 0, 1, 2, 3, …}.
A set can also be described in natural language using English phrases. For example, “the set of all positive integers” describes a particular set. It is important that the description be precise, so that there is no doubt about whether a particular object is or is not an element of the set. A common example of an imprecise description is a phrase such as “the numbers between 1 and 10.” This phrase has several ambiguities. Are the numbers 1 and 10 themselves elements of the set, or are they excluded? Are all real numbers between 1 and 10 included, or only the integers? Finally, the phrase should probably be clearer about the fact that these numbers are to be considered as a set, rather than individually. A more precise description of this set might be “the set of positive integers no greater than 10” (if the numbers 1 and 10 are in the set, and only whole numbers are included) or “the set of real numbers between 1 and 10, exclusive” (if the set includes numbers with fractional parts, but not the numbers 1 and 10 themselves).
The symbol ∈ is used to mean “is an element of,” just as the symbol = is used to mean “equals.” For example, to say that the number 2 is an element of the set {1, 2, 3}, we can write 2 ∈ {1, 2, 3}. To express the opposite, “is not an element of,” we put a slash through the symbol and write ∉. For example, we can write 4 ∉ {1, 2, 3}.
It is often useful to assign names to sets. These names are usually chosen to be single letters, similar to the use of letters to represent numbers in algebra. A very common convention is to use capital letters for the names of sets and lower-case letters to represent the elements of sets. So, for instance, if we assign the letter A to the set {1, 2, 3} by writing A = {1, 2, 3}, we can then say that 2 ∈ A. We can also write a ∈ A, by which we mean that a is a (possibly unknown) number that is an element of the set A—in other words, the value of a must be either 1, 2, or 3.
Two sets are said to be equal if every element of the first set is an element of the second set, and vice versa. For example, if A = {1, 2, 3} and B = {2, 3, 1}, then the sets A and B are equal. Every element of A is also an element of B, and every element of B is also an element of A. We express set equality with an equals sign, so in this case we write A = B. When two sets are equal, they are considered to be the same set. It is important to remember that equality between sets is a different concept than equality between numbers.
One consequence of this definition of equality is that the order in which the elements of a set are listed is irrelevant. We care only about which objects are elements of the set, not the order they come in. So, for instance, the expressions {1, 2, 3} and {2, 3, 1} both describe the same set.
Another consequence is that the number of times an element is listed is irrelevant. The set {1, 2, 1, 3, 3, 3} is equal to the set {1, 2, 3}, because every element of the first set is an element of the second, and vice versa. (It does not matter that the numbers 1 and 3 are listed several times in the first set.)
[Sometimes we need to use a collection of objects in which order is important. Such a collection is called a sequence or an ordered list. An example is the use of ordered pairs of the form (x, y) to represent points in a two-dimensional plane; the point (2, 5) is different from the point (5, 2). Similarly, we sometimes need a collection of objects in which it is meaningful for an element to appear more than once. Such a collection is called a multiset. When we refer to a set, however, it is to be understood that the order and repetition of the elements is irrelevant.]
The elements of a set can be anything—even other sets. For example, suppose we have two sets, A = {1, 2, 3} and B = {2, 3, 4, 5}. Think of A as a box containing the numbers 1, 2, and 3, and B as a box containing the numbers 2, 3, 4, and 5. There is nothing stopping us from putting the box A and the box B together inside a larger box C. In the same way, we can make a set C containing the set A and the set B as elements. We can write the set C as {A, B}, or, if we like, we can say
C = { {1, 2, 3}, {2, 3, 4, 5} }.
A set containing other sets is like a box containing other boxes. In this case, the set C has two elements, which are the two sets A and B. These elements of the set C are themselves sets; the set A has three elements, and the set B has four elements.
Therefore it is true that A ∈ C, because A is an element of C. Similarly, it is true that B ∈ C. Of course, it is also true that, say, 1 ∈ A, because the number 1 is an element of the set A.
However, it is not true that 1 ∈ C, because 1 is not an element of the set C. The only two elements of C are the sets A and B, and neither of these two elements is the number 1. (The set A contains the number 1, but A itself is not the number 1.)
Returning to the box metaphor, we should think about elements of a set (a box) as the objects that are directly inside the box. The number 1 is not directly inside the box C; instead, it is hidden inside the box A. So 1 is not an element of the set C, but 1 is an element of the set A.
Likewise, even though it is true that 2 ∈ A and also true that 2 ∈ B, it is not true that 2 ∈ C, because the number 2 is not directly inside the box C.
Now let’s consider the set
D = {1, 2, 3, 2, 3, 4, 5},
which is the same as the set {1, 2, 3, 4, 5} because the order and repetition of the elements are irrelevant. The set D is different from the set C—these sets are not equal. To see this, it is enough to find a single element in one set that is not an element of the other set. Well, the number 1, for example, is an element of D but (as explained above) is not an element of C; so the sets are not equal. Thinking of C and D as boxes, we see why they are not the same: the set C is a box that contains two boxes (which themselves happen to contain some numbers), whereas the set D is a box that directly contains five numbers (and no boxes).
As another example, consider the two sets E = {1} and F = {{1}}. These sets are not equal. The set E has one element, which is the number 1; the set F also has one element, but the single element of F is another set, not a number. So, whereas the set E is a box containing the number 1, the set F is a box containing a box containing the number 1. (In other words, the set F is a box containing E—do you see this?) Both of these are different from the number 1 itself. So it is true that 1 ∈ E, and in fact E ∈ F (because the single element of F is the set E), but it is not true that 1 ∈ F.
Sets containing other sets are common in some areas of mathematics, but we won’t see them very often in this course. (Mathematicians who work in these areas often call a set containing other sets a “collection of sets” or a “family of sets” to avoid the awkward phrase “set of sets.”)
The cardinality of a set is the number of elements that the set contains. (Sometimes the cardinality of a set is simply called the “size” of the set, because size is a shorter word; but “cardinality” is the technically correct term.)
It is common to write |A| to mean the cardinality of the set A. For example, if A = {1, 4, 8}, then |A| = 3, because A has three elements. This is the same notation as is used for the absolute value of a number, but context makes it clear what is meant: if the vertical bars surround a set, they refer to the cardinality of the set.
The cardinality of a set might be infinite. For instance, the cardinality of the set of positive integers, {1, 2, 3, …}, is infinite.
We have been thinking of sets as boxes. What kind of set corresponds to the idea of an empty box? Clearly it must be a set that contains no elements at all. We call such a set an empty set. Since any two empty sets contain exactly the same elements (specifically, no elements at all), we consider any two empty sets to be equal, and hence the same set. So we usually refer to the empty set, because there is really only one.
There are two common ways to write the empty set. The first way, as you might expect, is { }. The other notation is a circle or a zero with a slash through it, which looks like ∅. Both { } and ∅ are symbols for the empty set.
Note that there is a difference between ∅ and {∅}. The first is the empty set, which is an empty box. The second is a box containing an empty box, so the second box is not empty—it has a box in it! Don’t write {∅} when you mean the empty set, because {∅} refers to a set containing the empty set, which is not the same as the empty set itself.
The cardinality of the empty set is 0, which makes sense, because the empty set contains no elements. The statement x ∈ ∅ is always false, no matter what x is, because there is no such thing as an element of the empty set.
Above, we defined two sets A and B to be equal if every element of A is an element of B, and vice versa. If we remove the “vice versa” from this definition, we get the definition of a subset.
We say that a set A is a subset of a set B if every element of A is also an element of B. We use the symbol ⊆ to mean “is a subset of“; for example, A ⊆ B means “A is a subset of B.” We can also turn this symbol the other way and write the sets in the other order to get B ⊇ A; this means the same as A ⊆ B. To write that A is not a subset of B, we draw a slash through the subset symbol: A ⊈ B. Intuitively, a subset of B is a “part” of B.
For example, consider the sets C = {1, 2} and D = {1, 2, 3, 4}. The set C is a subset of D, because every element of C is also an element of D. So we can write C ⊆ D. A given set has many subsets; for example, another subset of D is {1, 3, 4}.
To remember which direction to write the symbol ⊆, think about the cardinalities of the sets and the inequality symbol ≤. If A is a subset of B, then B must contain at least as many elements as A does (simply because B contains all of the elements of A), so the cardinality of B must be greater than or equal to the cardinality of A. In other words,
A ⊆ B implies that |A| ≤ |B|.
Note that the symbols above “point” in the same direction.
There is a very important difference between the symbols ∈ and ⊆. The symbol ∈ is used to indicate an element of a set, whereas the symbol ⊆ is used to indicate a subset. For instance, consider the set
D = {1, 2, 3, 4}.
The set {2, 4} is a subset of D, because every element of {2, 4} is also an element of D, so it is correct to write {2, 4} ⊆ D. But the set {2, 4} is not an element of the set D, because the four elements of the set D are all numbers (D does not have any sets as elements), so it is incorrect to write {2, 4} ∈ D. On the other hand, the number 2 is an element of D, so it is correct to write 2 ∈ D; but the number 2 is not a subset of D (because the number 2 is a number, not a set), so it is incorrect to write 2 ⊆ D. If we want to refer to the subset of D containing only the number 2, we should write {2}, which is the set containing 2 (note that the set {2} is different from the number 2). The set {2} is a subset of D, that is, {2} ⊆ D; but it is not an element of D, because D does not have any sets as elements, so it is incorrect to write {2} ∈ D.
When A is a subset of B, the set B is occasionally called a superset of A. We can also say “B contains A as a subset,” but great care should be taken with the word “contains,” because, as noted in the previous paragraph, there is a big difference between saying “B contains A as an element” (meaning A ∈ B) and saying “B contains A as a subset” (meaning A ⊆ B). I will try to use the word contains only to refer to elements, not subsets.
A careful reading of the definition of subset shows that every set is a subset of itself. For example, using the set D from above, it is obviously true that “every element of D is also an element of D,” so by definition D is a subset of D. We often want to exclude this case, so we define a proper subset of a set B to be a subset of B that is not B itself. We write A ⊂ B to mean that A is a proper subset of B. [This usage of the symbols ⊆ and ⊂ to mean “is a subset of (or equal to)” and “is a proper subset of,” respectively, parallels the usage of the inequality symbols ≤ and < to mean “is less than or equal to” and “is strictly less than,” respectively.]
The empty set is considered to be a subset of every set (including itself). This may seem like a rather odd convention. Perhaps the best justification for it comes from turning the definition of subset on its head and asking what it means for a set A not to be a subset of B. From the definition, this must mean that there is some element in A that is not an element of B. So what would it mean to say that the empty set is not a subset of B? It would mean that there is some element in the empty set that is not an element of B—but this cannot be true, because there are no elements in the empty set! So, from this point of view, it makes some amount of sense to say that the empty set is a subset of every set.
[It should be noted that the usage of the symbols ⊆ and ⊂ described above is not universal. Some authors use the symbol ⊂ to mean “is a subset of” (for which we are using the symbol ⊆) and introduce a new symbol ⊊, a subset symbol with the “equals” bar crossed out, to mean “is a proper subset of” (for which we are using the symbol ⊂).]
There are some sets of numbers that are so commonly useful that they have special symbols. Double-struck capital letters, sometimes called blackboard bold letters, are often used (in particular, the letters ℝ, ℤ, ℕ, and ℚ). Alternatively, the letters may simply be typeset in boldface. [Due to the possibility that unusual symbols, such as blackboard bold, may not appear correctly in all Web browsers, I will use simple boldface letters here.]
The set of all real numbers, both positive and negative (and zero), is called R (for “real”). The set of real numbers includes all numbers commonly encountered in an algebra, trigonometry, or calculus course. (It does not contain complex numbers such as √−1.)
The set of integers (positive, negative, and zero) is called Z (from the German word Zahlen, meaning “numbers”). In other words, Z = {…, −3, −2, −1, 0, 1, 2, 3, …}.
The set of natural numbers is called N (for “natural”). The set of natural numbers contains all positive integers and no negative integers. Unfortunately, there is no consensus on whether zero should be considered a natural number. Some authors include 0 in the set N, while others do not. The reason for this lack of consistency is that sometimes it is useful to include zero and sometimes not, depending on the situation. So mathematicians use whichever definition suits them best at the time—but they are aware of the differences in usage, so they are always very careful to state exactly which definition they are using in any particular case to avoid any confusion or ambiguity, and once they have decided on a definition they stick with it. For this class, let’s agree that 0 is not a natural number unless specified otherwise. In other words, unless otherwise stated, we will use the symbol N to represent the set {1, 2, 3, …}. If we wish to refer to the set {0, 1, 2, 3, …} when we are using this definition of N, we can always write N ∪ {0} (we’ll talk about the meaning of the symbol ∪ in a bit). Alternatively, the terms positive integer and non-negative integer are always unambiguous: zero is not positive, but it is non-negative. Therefore, another way to refer to the set {1, 2, 3, …} is “the set of positive integers,” while {0, 1, 2, 3, …} is “the set of non-negative integers.”
Finally, the set of rational numbers is called Q (from the word “quotient”). A rational number is a number that can be written exactly as a fraction, or quotient, of two integers. For example, the number 2/3 is a rational number, as is the number −7/2. All integers are rational numbers, because any integer can be written as a fraction with denominator 1; for instance, the integer 5 can be written as 5/1. Other examples of rational numbers include numbers that can be written as a terminating decimal (for example, the number 8.13 can be written as 813/100) or as a repeating decimal (for example, the number 0.333… can be written as 1/3). Not all real numbers are rational, however. Examples of real numbers that cannot be written exactly as a fraction of two integers include √2 and π; the decimal expansions of these numbers go on forever and never repeat. In this course we will not have much of a need to distinguish rational numbers from real numbers, so we will rarely (if ever) use the symbol Q.
Note that these four sets of numbers are (proper) subsets of each other: N ⊂ Z ⊂ Q ⊂ R.
Listing all of the elements of a set is fine as long as the set is not too big. For larger sets, we can skip some of the elements by writing an ellipsis (…), as we have seen, but this is only feasible when the elements follow a pattern that can be clearly seen in the first few elements. This is not always the case. For example, the set of all prime numbers between 100 and 500 could be written as {101, 103, 107, …, 499}, but this is not a very helpful thing to write because it is very difficult to guess the correct pattern from these numbers alone (and this expression does not rule out incorrect patterns such as “the set of all odd numbers between 100 and 500, except multiples of 5”).
In situations like this, it is often better to describe a set by specifying a condition for membership. (Our English description of the set above does exactly this; it says, in effect, that the condition for a number to an element of the set is that the number must be prime and between 100 and 500.) When we want to describe a set in this way, we can use set-builder notation.
When we use set-builder notation, we must first establish the universal set (sometimes called the domain of discourse or the universe of discourse), which is the set of all possible objects under consideration. For example, we might say that the universal set is R, the set of all real numbers; or perhaps Z, the set of integers. Another possibility is to use a previously defined set as the universal set. If we have defined A = {1, 2, 3}, for instance, we can use A as the universal set.
Once we have chosen a universal set, we may “build” a set by choosing all of the elements of the universal set that satisfy a specified condition. For example, if the universal set is R, we can define a set B to be, say, the set of all elements of R that are greater than 17. (So B contains the numbers 18 and 29.4, for example, but does not contain 11.26 or −30.) This set B can be written using set-builder notation as
B = { x ∈ R | x > 17 }.
In set-builder notation, the vertical bar | should be read as “such that” or “satisfying the condition that.” So the expression above can be read as “B is the set that contains every element x in the universal set R satisfying the condition that x > 17.”
Note that the universal set is specified on the left side of the vertical bar, and a name is given to represent an arbitrary element of the universal set by using the symbol ∈. On the right side of the bar is the condition that the element must satisfy in order to be a member of the set we are building. The name for the arbitrary element (x in the example above) can be anything; the example above means exactly the same as, say,
B = { z ∈ R | z > 17 },
or even
B = { ♣ ∈ R | ♣ > 17 },
though ♣ is not a very common variable name (and it is likely to cause some amount of puzzlement, so it should probably be avoided).
Why is the universal set important? The answer is that a set described using set-builder notation will always be a subset of the universal set. Consider the set
C = { x ∈ N | x > 17 },
which is defined in exactly the same way as the set B above except that the universal set has been changed to N. The sets B and C have many elements in common; for example, the number 20 is an element of both B and C. However, since C has been built out of elements of N rather than elements of R, the set C contains only (positive) integers and does not contain any number with a fractional part. So, for instance, the number 23.456 is an element of B but is not an element of C.
As another example of set-builder notation, consider the set
D = { n ∈ N | n ≤ 10 }.
What does this mean? Reading from left to right, one symbol at a time, we read, “D is the set that contains every element n in the universal set N satisfying the condition that n ≤ 10.” Here, the universal set is the set N of natural numbers (which we have agreed does not include 0), so we see that
D = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}.
Note that a set described using set-builder notation might be empty, if no elements in the universal set satisfy the specified condition! For example, the set
E = { n ∈ N | n < 0 }
is the empty set, because there are no natural numbers less than zero. A somewhat more subtle example of a set that turns out to be empty is
F = { n ∈ N | 8 < n < 9 },
which is empty because there is no natural number n that satisfies the inequality 8 < n < 9. (Recall that 8 < n < 9 is shorthand for “8 < n and n < 9.” No natural number satisfies this condition because every natural number is either less than or equal to 8, or greater than or equal to 9.)
The condition in set-builder notation does not need to be written in mathematical symbols. It is common for the condition to be written as an English phrase. For example, we can define S to be the set of perfect squares by writing
S = { t ∈ Z | t is a perfect square }.
(We used Z as the universal set here instead of N, even though no negative integer is a perfect square, because zero is a perfect square and we wanted to include it in the set S. This is an instance in which it would have been convenient for 0 to be in N. Oh well.)
If the universal set is specified explicitly in words either before or after the use of set-builder notation, it is often omitted in the set-builder notation itself. For example, when defining several sets, we may say:
Let
K = { x | x ≠ 0 }, L = { x | −6 ≤ x < 1 }, M = { x | x ≥ 50 and x is perfect }, where the universal set is the set of real numbers.
In this case, since the universal set is specified to be the set of real numbers, we should read the definition of the set K as “K is the set that contains every real number x satisfying the condition that x ≠ 0.” In other words, K is the set of all real numbers except 0. Can you understand the definitions of L and M?
Occasionally a colon (:) is used instead of the vertical bar in set-builder notation. This is especially common when the condition involves an absolute value expression, because the vertical bars used in the absolute value notation can be easily confused with the vertical bar used in the set-builder notation.
There are several operations that can be performed on sets in order to get new sets from old ones. These operations are as fundamental to set theory as addition and multiplication are to arithmetic.
Let’s consider the sets
| A | = | {1, 2, 3, 5, 8, 13}, |
| B | = | {2, 4, 6, 8, 10}. |
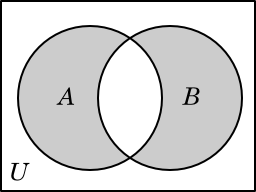
One useful thing to be able to do with these sets is to “put them together”—in other words, to make a new set that contains every element of A and also every element of B. Such a set is called the union of A and B, and is written A ∪ B. In this example, we have
A ∪ B = {1, 2, 3, 4, 5, 6, 8, 13}.
Note that the numbers 2 and 8 are each contained in both A and B, but they are each listed only once in A ∪ B, because the number of times an element is listed in a set is irrelevant.
No matter what the sets A and B are, it is always true that A ⊆ (A ∪ B) and B ⊆ (A ∪ B). Do you see why?
Another useful operation is to pick out the elements that A and B have in common. This is called the intersection of A and B, and is written A ∩ B. In our current example, we have
A ∩ B = {2, 8}.
No matter what the sets A and B are, it is always true that (A ∩ B) ⊆ A and (A ∩ B) ⊆ B. Do you see why?
If the sets A and B have no elements in common, they are said to be disjoint. In this case the intersection A ∩ B is the empty set.
Suppose one of the two sets we are working with is the empty set. No matter what the set A is, it is always true that A ∪ ∅ = A and A ∩ ∅ = ∅. Do you see why?
Another useful thing to do with a set is to consider everything that is not in the set. In order to have a precise meaning for “everything,” we need to specify a universal set (as we did when using set-builder notation). The set of all elements of the universal set that are not elements of a set A is called the complement of A, and is written A. (Another common notation for the complement of A is Ac.)
For example, suppose the universal set is N. Let P be the set of primes; that is,
P = { n ∈ N | n is prime } = {2, 3, 5, 7, 11, 13, 17, …}.
Then P, the complement of P, is the set of composite numbers (and the number 1, which is neither prime nor composite):
P = {1, 4, 6, 8, 9, 10, 12, …}.
Occasionally we have a need to refer to all of the elements in some set A that are not elements of some other set B. This operation is called the set difference (sometimes called the relative complement), and is written A \ B. (Some authors use a standard minus sign and write A − B, but the operation of set difference is quite different from the ordinary idea of subtraction, so the backslash is more common.)
For instance, if we have the sets
| A | = | {3, 4, 5, 10, 14, 17}, |
| B | = | {4, 5, 17}, |
then the set difference A \ B is
A \ B = {3, 10, 14},
because these are the elements of A that are not elements of B.
It is not necessary that either set be a subset of the other. For example, consider the sets
| C | = | {1, 3, 6, 10, 15}, |
| D | = | {1, 4, 5, 6, 10, 20}. |
Neither of these sets is a subset of the other. The set difference operation is still meaningful, however. We have
C \ D = {3, 15},
because these are the elements of C that are not elements of D; and
D \ C = {4, 5, 20},
because these are the elements of D that are not elements of C.
Note that, if the universal set is called U, then we can express the complement of a set A as a set difference:
A = U \ A.
Let’s think about how the empty set behaves with the set difference operation. No matter what the set A is, it is always true that A \ ∅ = A and ∅ \ A = ∅. Do you see why?
When we perform two or more set operations, we often need to include parentheses to make the order of evaluation unambiguous. For example, suppose we have the sets
| A | = | {1, 2, 3}, |
| B | = | {2, 3, 4}, |
| C | = | {3, 4, 5}. |
Let’s consider the expression (A ∪ B) ∩ C. We evaluate A ∪ B first, because it’s in parentheses. We see that A ∪ B = {1, 2, 3, 4}, so
(A ∪ B) ∩ C = {1, 2, 3, 4} ∩ C = {3, 4}.
On the other hand, suppose we have the expression A ∪ (B ∩ C), which is exactly the same except for the placement of the parentheses. Here we evaluate B ∩ C first, which is {3, 4}, so we get
A ∪ (B ∩ C) = A ∪ {3, 4} = {1, 2, 3, 4}.
This example shows that the placement of parentheses is important. Parentheses are free—if you’re unsure about whether you need parentheses in an expression, put them in just to be safe.
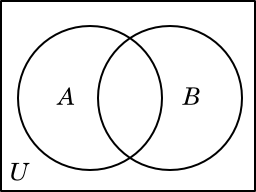
Venn diagrams, introduced by the English mathematician John Venn in 1881, are very useful for understanding the relationships between sets.
In a Venn diagram, sets are represented with overlapping shapes. The outermost shape, which is conventionally a rectangle, represents the universal set. Inside this rectangle are other shapes (often circles) representing various sets. These shapes may overlap, indicating the possibility that two or more sets may have some elements in common.
Shown below is the most common way to draw a Venn diagram for two sets, A and B. Here the universal set is called U.

For example, suppose the universal set is
U = {1, 2, 3, …, 12}
and we define the sets
| A | = | {1, 2, 3, 7, 9, 11}, |
| B | = | {3, 4, 7, 11}. |
The Venn diagram below shows the integers from 1 through 12 in the appropriate places. For instance, the number 1 is inside the circle labeled A but outside the circle labeled B, because 1 is an element of A but not of B. The number 7 is inside both of the circles, because it is an element of both A and B. The number 5 is inside the rectangle, because it is an element of the universal set, but it is outside both circles, because it is in neither A nor B.
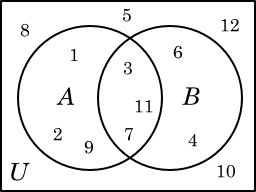
From this diagram, it is easy to see, for instance, that A ∩ B = {3, 7, 11}.
A Venn diagram is especially useful when we are thinking about abstract or unknown sets, rather than specific examples such as the sets above. In this case we cannot write the elements of the sets explicitly; instead we imagine the various areas of the diagram itself as metaphors for the various sets we are working with. It is helpful to shade or color parts of the diagram to highlight certain areas.
The shaded areas in the diagrams below show the areas corresponding to the indicated sets.
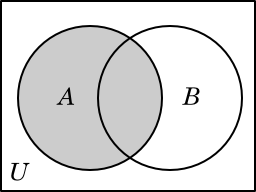 A |
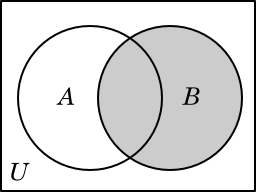 B |
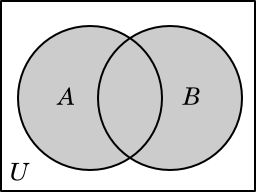 A ∪ B |
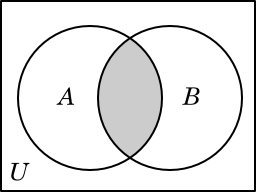 A ∩ B |
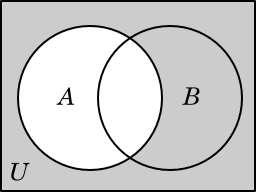 A |
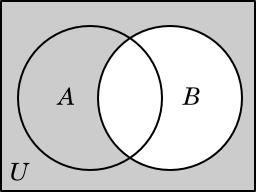 B |
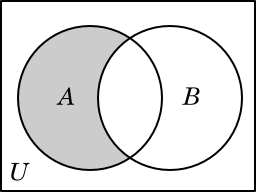 A \ B |
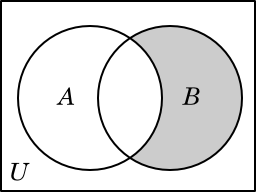 B \ A |
One use of Venn diagrams is to verify that two expressions actually describe the same set. For example, consider the two expressions
(A ∪ B) \ (A ∩ B) and (A \ B) ∪ (B \ A).
Let’s draw Venn diagrams for these sets. We’ll start with the expression on the left. The Venn diagrams for A ∪ B and A ∩ B are shown below.
 A ∪ B |
 A ∩ B |
Now the shaded area in the Venn diagram for (A ∪ B) \ (A ∩ B) should include the areas that are shaded in the Venn diagram for A ∪ B but not shaded in the Venn diagram for A ∩ B. So the Venn diagram for (A ∪ B) \ (A ∩ B) looks like this:
 (A ∪ B) \ (A ∩ B) |
Let’s consider the other expression now: (A \ B) ∪ (B \ A). The Venn diagrams for A \ B and B \ A are shown below.
 A \ B |
 B \ A |
Now the shaded area in the Venn diagram for (A \ B) ∪ (B \ A) should include the shaded area in the Venn diagram for A \ B and also the shaded area in the Venn diagram for B \ A. So the Venn diagram for (A \ B) ∪ (B \ A) looks like this:
 (A \ B) ∪ (B \ A) |
Note that this is exactly the same Venn diagram as we obtained for (A ∪ B) \ (A ∩ B). This shows that these two expressions are different ways of naming the same set. In other words, for any two sets A and B, it is true that
(A ∪ B) \ (A ∩ B) = (A \ B) ∪ (B \ A).
(This set is sometimes called the symmetric difference of A and B, written A Δ B.)
Here are some questions about sets to check your understanding.